An Introduction to A/B Testing (Part 4) - How long should an A/B test run?

How long should an A/B test run?

This is the conclusion of our A/B testing series. The previous article can be found at An Introduction to A/B Testing (Part 3) - Measuring Results.

There are three factors that control how long your test should be run:

• how much does your conversion rate bounce around?
• how long does it take prospects to convert?
• how much data is needed for statistical significance?

How much does your conversion rate bounce around?

Since you are measuring human activity, it is reasonable to expect that different unknown sub-groups in both your test and control groups will convert at different rates and that there will be variance in the conversion rate within each group over time.

For example, a group of 1,000 customers with an average conversion rate of ≈26% can look meaningfully different when the “win rate” is averaged over different time intervals.

Below are plots of the moving average of the “win rate” averaged over n samples at a time.

The takeaway here is that even if your test shows as statistically significant, your results may be reflecting a hill or valley that is different from the longer term rate. It’s often useful to graph the conversion rates of previous prospects who are not part of the test, averaged over time windows equal to your test duration, to see how much they bounce around. If the 95% window often extends above the level of improvement seen, it is wise to either run the test longer (with more data) or to run the test again.

How long does it take prospects to convert?

Another consideration in your design is how long it takes prospects to convert.

The approach you take for determining when to measure the conversions from the experiment will depend upon the time scale of the conversion.

Case #1 - short time frame - Open/click rate

Below is a histogram of count (the number of conversions) vs. action time (the number of days between receipt and action) and a density plot showing the shape of the responses (the black vertical line represents the average; the curve represents the idealized “normal” relationship between count and time).

Even though we’re seeing two peaks, for reasonably short conversion time windows, we recommend assuming the data would peak around one value if we had more data (the “normal” assumption).

With this assumption, our advice is to measure conversions at a time greater than when 95% of your conversions are likely to be made. (Remember to count this time from when the last email was sent as many email marketing system spread out when the sends occur to avoid SPAM labels). (The data is what is called “right censored” — data collection stopped and analysis was done before all of the conversions (further to the right on the time axis) were completed.)

We recommend making a bar chart/histogram before computing any statistics.

To calculate the cut-off time:

Mean (a.k.a. average):

Standard deviation:

95% window:

So, for the example data graphed above, the cut-off time for measuring a conversion should be sometime after 10 days.

Case #2 - long conversion time - Sales

Long time windows are problematic and should be avoided as much as possible.

We often find that there are at least three time arcs that prospects follow. The mixing of these three groups makes it very difficult to establish a usable/palatable average time between prospect creation and sale.

Below is a fairly typical “days to sale/win” graph and a density graph.

There is more than one peak, indicating a mixture of conversion time arcs.

This generally happens when customers become leads at different points in the conversion funnel.

purchase funnel

Some prospects don’t become leads until they are near purchasing; some do it very early; others enter somewhere in the middle.

If you torture the data long enough, it will confess.

– Ronald Coase

It is sometimes possible to perform an analysis on the sale days to try to “split” what is being observed into different time-to-sell groups. If it is possible to assign test participants into different time groups before the experiment is run, then separate A/B tests should be performed for each group.

It is useful to make a graph of the cumulative sales as a function of account age:

Although 1-2 months is probably a bearable test duration, 5+ months is not.

You should measure and assess how each group in an A/B test performs with respect to all goals; you should not, however, use a long-time-frame conversion as the conversion for assessing an A/B test — pick an earlier milestone.

You can begin analysis of the long-term goal once more than 50% of the data is in. Our advice would be to repeat the analysis at ~10% steps. If the results seem fairly stable, you can compute a χ2 to determine if you are seeing a significant difference between the two groups. If you are, you can the report the difference with a margin of error.

Statistical significance

Do not put your faith in what statistics say until you have carefully considered what they do not say. – William W. Watt

Never report insignificant results.

The biggest mistake organizations that are doing testing make is acting on insignificant results. This is very dangerous.

The math to figure out if you have good numbers is pretty simple. Put your numbers into a table like this:

It is okay to flip the order of the rows, the order of the columns and to transpose the rows for columns. The statistic does not require that the number of reported test and control results be the same.

Now, calculate something called a χ2 (“chi-squared”) statistic as follows:

If you go look up χ2 test on Wikipedia and the related χ2 distribution, you will see some pretty ugly-looking equations. If you spend a few hours doing the algebra, you will end up with the form we’re using in this article.

If your result is bigger than 3.8414588, then your test and control group results are significantly different with 95% or better confidence.

At 95% confidence, there is 1/20 chance that there is no difference between your test and control groups. At 99% confidence, there is a 1/100 chance that there is no difference between your two groups.

We recommend using 95% as the significance threshold for marketing A/B tests.

Below is a list ofvalues with different significance levels:

χ2 value	significance
3.8414588	95%
6.6348966	99%
10.8275662	99.9%
15.1367052	99.99%
19.511421	99.999%

Distribution

As shown below, low 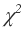values have low significance. The higher the value, the stronger your results.

Sanity check – Test 1/2of each group against the other 1/2

You should always perform an anti-experiment to make sure nothing is amiss in the process.

Split each group in half and do a on one half versus the other — an A/A and a B/B test. Your expectation is that each test should come back as insignificant (i.e. A1 performs the same way A2 performs and B1 performs the same way B2 performs).

You should NOT see statistical significance.

If you do see significant differences in your A/A or B/B test, you should first check experimental setup and your data collection; if both are okay, then your experiment should run longer.

Test Size

The starting win rate and the amount of improvement being observed directly influence the amount of observations you need in order to have significant results.

The results from larger experiments are more significant than those from smaller experiments (at the same success rates for each experimental group).

As an example, the table below lists the win-rate improvement, the value, the p-value (1 minus p-value = significance level; you want a p-value ≤ 0.05) and whether or not the data has statistical significance for an A/B test where the Control Group has a win rate of 25% and theTest Group has a win-rate of 35% — an improvement of 10%.

Group Size	Control Wins	Test Wins	improvement range [%]		p-value	significant?
100	25	35	-2.69 - 22.69	2.380952	0.1228226	FALSE
150	37	52	-0.34 - 20.34	3.594441	0.0579731	FALSE
200	50	70	1.05 - 18.95	4.761905	0.0290963	TRUE
250	62	87	2.00 - 18.00	5.975258	0.0145080	TRUE
300	75	105	2.70 - 17.30	7.142857	0.0075263	TRUE

As you can see, once the test has 200 observations in both experimental groups, the results become significant.

The good news for A/B testers is that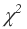values increase (assuming that the win rates remain the same) as the number of observations increases.

To figure out approximately how many control and test group samples you will need to collect for significance once you have collected some data, you can use the following “trick”:

• Let p be the win rate of the control group (in the range of 0 to 1 (i.e. divide the percentage by 100))
• Let α be the improvement (or worsening) in the win rate in the test group (this should be in the range 0<α≤1−p)
• Calculate an approximate N value via this equation  
• Substutute in the value offor the significance level you want. For example, at 95% confidence, χ2=3.8414588, which yields the equation:

 

For p=0.25and α=0.10,

The 10% improvement case matches up with the finding above that somewhere between N=150and N=200, the results from the experiment with a 25% control group win rate and a 35% test group win rate become significant. 

Smaller improvements will require larger group sizes.

1. The values of p and α will change as you run the experiment – the value of N required may shift;
2. N as used here is the size of the test and control groups separately – the size of the total experiment is 2N.

Below are some graphs to give you a general sense of how significance is impacted by test size, control win rate and test improvement rate. Our goal is to give you a general sense of how different values for these variables impacts test significance.